前言

本笔记用于记录刷题过程中遇到的中等及以上难度的题和一些特殊算法思想，语言大部分会用 JavaScript 来刷题，也有的会用C++和Java

承接算法笔记（三），继续刷LeetCode75，同时也做每日一题，进行算法扫盲

LeetCode75完结！

题库LeetCode75

本题库涉及到的知识点一览

• [x] 数组 / 字符串
• [x] 双指针
• [x] 滑动窗口
• [x] 前缀和
• [x] 哈希表 / 哈希集合
• [x] 栈
• [x] 队列
• [x] 链表
• [x] 二叉树 - 深度优先搜索
• [x] 二叉树 - 广度优先搜索
• [x] 二叉搜索树
• [x] 图 - 深度优先搜索
• [x] 图 - 广度优先搜索
• [x] 堆 / 优先队列
• [x] 二分查找
• [x] 回溯
• [x] 动态规划 - 一维
• [x] 动态规划 - 多维
• [x] 位运算
• [x] 前缀树
• [x] 区间集合
• [x] 单调栈

---

198.打家劫舍

题目：

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

---

解析：

经典dp，状态方程dp[i]=max(dp[i-2]+nums[i],dp[i-1])

//copy灵神极致简洁代码
var rob = function (nums) {
    let f0 = 0, f1 = 0;
    for (const x of nums) {
        [f0, f1] = [f1, Math.max(f1, f0 + x)]
    }
    return f1;
};

431.路径求和Ⅲ

题目：

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

---

解析：

我的想法是先用dfs遍历，然后每个节点记录一下当前位置到根节点的路径上所有节点和，就是前缀和，但是没想好怎么用数据结构存储前缀和以及怎么确定节点是某一个节点的祖先。看了官解，用的是Map，记录的不是节点，而是某一个前缀和出现的次数，每次遍历了一个节点的路径会恢复状态查询其他路径

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
    let presum=new Map();
    presum.set(0,1);
    const dfs=(root,presum,targetSum,cur)=>{
        if(root==null){
            return 0;
        }
        let res=0;
        cur+=root.val;
        //查找是否有符合的前缀和
        res=presum.get(cur-targetSum)||0;
        presum.set(cur,(presum.get(cur)||0)+1);
        res+=dfs(root.left,presum,targetSum,cur)+dfs(root.right,presum,targetSum,cur);
        //这里是把下面所有节点遍历后，恢复原来状态，搜索其他路径
        presum.set(cur,presum.get(cur)-1);
        return res;
    }
    return dfs(root,presum,targetSum,0);
};

236.二叉树的最近公共祖先

题目：

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

---

解析：

本题在于递归的思路
若 root 是 p,q的 最近公共祖先 ，那么只有三种情况
p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
p=root ，且 q 在 root的左或右子树中；
q=root ，且 p 在 root 的左或右子树中；

先自顶向下遍历，遇到节点p或者q返回，然后自底向上回溯，第一个符合的root就是最近公共祖先

var lowestCommonAncestor = function (root, p, q) {
    if (root == null || root == p || root == q) {
        return root;
    }
    const left = lowestCommonAncestor(root.left, p, q);
    const right = lowestCommonAncestor(root.right, p, q);
    //p 和 q 都不在 root 的子树中，继续向上回溯
    if(left==null&&right==null){
        return null;
    }
    //左子树为空，那么p和q肯定在右子树里(一个在或者都在)
    if(left==null){
        return right;
    }
    //右子树为空，那么p和q肯定在左子树里(一个在或者都在)
    if(right==null){
        return left;
    }
    //p 和 q 在 root 的子树中
    return root; 
};

994.腐烂的橘子

题目：

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：
值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

---

解析：

多源bfs，和1926的迷宫很像，但是要注意这两个题都是同一时刻多点进行bfs，不一定是一条路径上或者联通的，所以要有两个while，第二个while是用于清空每一时刻queue里的值，这些是同时发生的

/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function (grid) {
    const direction = [[0, -1], [-1, 0], [0, 1], [1, 0]];
    let queue = [];
    let fresh = 0;
    let rows = grid.length, cols = grid[0].length;
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (grid[i][j] == 1) {
                fresh++;
            }
            //把所有腐烂橘子都加入队列
            if (grid[i][j] == 2) {
                queue.push([i, j]);
            }
        }
    }
    let minutes = 0;
    while (queue.length != 0 && fresh) {
        let len = queue.length;
        //这里一定要注意把queue当前的长度抽取出来，这是把同一分钟的腐烂橘子都一起向四周污染，如果不单独while的话会漏掉同一时间的腐烂橘子
        while (len--) {
            let cur = queue.shift();
            for (dir of direction) {
                let curi = dir[0] + cur[0], curj = dir[1] + cur[1];
                if (curi >= 0 && curi < rows && curj >= 0 && curj < cols && grid[curi][curj] == 1) {
                    grid[curi][curj] = 2;
                    queue.push([curi, curj]);
                    fresh--;
                }
            }
        }
        minutes++;
    }
    return fresh == 0 ? minutes : -1;
};

2009.使数组连续的最少操作数

题目：

给你一个整数数组 nums 。每一次操作中，你可以将 nums 中 任意 一个元素替换成 任意 整数。
如果 nums 满足以下条件，那么它是 连续的 ：
nums 中所有元素都是 互不相同 的。
nums 中 最大 元素与 最小 元素的差等于 nums.length - 1 。
比方说，nums = [4, 2, 5, 3] 是 连续的 ，但是 nums = [1, 2, 3, 5, 6] 不是连续的 。
请你返回使 nums 连续 的 最少 操作次数。

---

解析：

滑动窗口问题，先排序，再每个数字都作为最小值试一下最少的操作数

var minOperations = function(nums) {
    const n = nums.length;
    const sortedUniqueNums = [...new Set(nums)];
    sortedUniqueNums.sort((a, b) => a - b);
    let res = n;
    let j = 0;
    for (let i = 0; i < sortedUniqueNums.length; i++) {
        const left = sortedUniqueNums[i];
        const right = left + n - 1;
        while (j < sortedUniqueNums.length && sortedUniqueNums[j] <= right) {
            res = Math.min(res, n - (j - i + 1));
            j++;
        }
    }
    return res;
};

1766.互质树

题目：

给你一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1 ，且恰好有 n - 1 条边，每个节点有一个值。树的 根节点 为 0 号点。
给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。
当 gcd(x, y) == 1 ，我们称两个数 x 和 y 是 互质的 ，其中 gcd(x, y) 是 x 和 y 的 最大公约数 。
从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。
请你返回一个大小为 n 的数组 ans ，其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ，如果不存在这样的祖先节点，ans[i] 为 -1 。

---

解析：

dfs，先暴力得到1-50内所有互质的元素集合gcds，然后后面对节点dfs，比较当前值gcds数组元素是否已经在前面的祖先节点出现过，然后再把当前的值对应位置存入tmp中

var getCoprimes = function(nums, edges) {
    const n = nums.length;
    const gcds = Array.from({ length: 51 }, () => []);
    const tmp = Array.from({ length: 51 }, () => []);
    const ans = Array(n).fill(-1);
    const dep = Array(n).fill(-1);
    const g = Array.from({ length: n }, () => []);

    function gcd(a, b) {
        while (b !== 0) {
            [a, b] = [b, a % b];
        }
        return a;
    }

    function dfs(x, depth) {
        dep[x] = depth;
        for (const val of gcds[nums[x]]) {
            if (tmp[val].length === 0) continue;
            const las = tmp[val][tmp[val].length - 1];
            if (ans[x] === -1 || dep[las] > dep[ans[x]]) {
                ans[x] = las;
            }
        }
        //遍历过就把当前值对应的位置存进tmp，后面找互质就直接找的等于该值的最后一个位置，也就是最近祖先
        tmp[nums[x]].push(x);
        for (const val of g[x]) {
            if (dep[val] === -1) { // 被访问过的点dep不为-1
                dfs(val, depth + 1);
            }
        }
        //边没有指明方向，所以回溯的时候要把当前的弹出来
        tmp[nums[x]].pop();
    }

    // 初始化
    for (let i = 1; i <= 50; i++) {
        for (let j = 1; j <= 50; j++) {
            if (gcd(i, j) === 1) {
                gcds[i].push(j);
            }
        }
    }
    //这里是因为不知道边的方向，要等到遍历的时候才知道
    for (const [x, y] of edges) {
        g[x].push(y);
        g[y].push(x);
    }

    dfs(0, 1);
    return ans;
};

1372.二叉树中的最长交错路径

题目：

给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：
选择二叉树中 任意 节点和一个方向（左或者右）。
如果前进方向为右，那么移动到当前节点的的右子节点，否则移动到它的左子节点。
改变前进方向：左变右或者右变左。
重复第二步和第三步，直到你在树中无法继续移动。
交错路径的长度定义为：访问过的节点数目 - 1（单个节点的路径长度为 0 ）。
请你返回给定树中最长 交错路径 的长度。

---

解析：

难得纯自己写了一次超越100%，思路蛮简单的，就是dfs，每个节点判断一下是向左还是向右，记录长度最大值即可

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var longestZigZag = function(root) {
    let max=0;
    const dfs=(root,len,dir)=>{
        max=Math.max(max,len);
        if(dir=="left"&&root.left!=null){
            dfs(root.left,len+1,"right");
        }
        if(dir=="right"&&root.right!=null){
            dfs(root.right,len+1,"left");
        }
        if(dir=="left"&&root.right!=null){
            dfs(root.right,1,"left");
        }
        if(dir=="right"&&root.left!=null){
            dfs(root.left,1,"right");
        }
    }
    dfs(root,0,"left");
    dfs(root,0,"right");
    return max;
};

1466.重新规划路线

题目：

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。
路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。
请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

---

解析：

这个题目就是把有向图变成以城市0为根的树，每个节点遍历能不能到城市0不好做，改成反向城市0能不能遍历到所有节点，能遍历过去的边代表实际中要反向，累加一下返回即可

/**
 * @param {number} n
 * @param {number[][]} connections
 * @return {number}
 */
var minReorder = function(n, connections) {
    const graph=new Array(n).fill(0).map(()=>new Array());
    for(const edge of connections){
        //这里按照一个点能到达所有点来构造邻接表
        //正向到达被记为1，反向为0(后面要累积正向的)
        graph[edge[0]].push([edge[1],1]);
        graph[edge[1]].push([edge[0],0]);
    }
    const dfs=(cur,parent)=>{
        let res=0;
        //对于当前节点遍历以其为起点的所有边
        for(const edge of graph[cur]){
            //如果当前边的终点是当前节点的父节点，证明已访问过，跳过，进入下一循环
            if(edge[0]==parent){
                continue;
            }
            //正向到达的实际上需要反向，所以累计加
            //递归访问当前边的终点节点
            res+=edge[1]+dfs(edge[0],cur);
        }
        return res;
    }
    return dfs(0,-1);
};

399.除法求值

题目：

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。
注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。
注意：未在等式列表中出现的变量是未定义的，因此无法确定它们的答案。

---

解析：

这道题像是hard的medium

1. 建表
   把所有的点建模成一张图，边代表两个变量的比值

var calcEquation = function(equations, values, queries) {
    let nvars = 0;
    const variables = new Map();
    //这一步是把字母先映射成数字
    const n = equations.length;
    for (let i = 0; i < n; i++) {
        if (!variables.has(equations[i][0])) {
            variables.set(equations[i][0], nvars++);
        }
        if (!variables.has(equations[i][1])) {
            variables.set(equations[i][1], nvars++);
        }
    }

    // 对于每个点，存储其直接连接到的所有点及对应的权值
    const edges = new Array(nvars).fill(0);
    for (let i = 0; i < nvars; i++) {
        edges[i] = [];
    }
    for (let i = 0; i < n; i++) {
        const va = variables.get(equations[i][0]), vb = variables.get(equations[i][1]);
        edges[va].push([vb, values[i]]);
        edges[vb].push([va, 1.0 / values[i]]);
    }

    const queriesCount = queries.length;
    const ret = [];
    for (let i = 0; i < queriesCount; i++) {
        const query = queries[i];
        let result = -1.0;
        if (variables.has(query[0]) && variables.has(query[1])) {
            const ia = variables.get(query[0]), ib = variables.get(query[1]);
            if (ia === ib) {
                result = 1.0;
            } else {
                const points = [];
                points.push(ia);
                const ratios = new Array(nvars).fill(-1.0);
                ratios[ia] = 1.0;

                while (points.length && ratios[ib] < 0) {
                    const x = points.pop();
                    for (const [y, val] of edges[x]) {
                        if (ratios[y] < 0) {
                            ratios[y] = ratios[x] * val;
                            points.push(y);
                        }
                    }
                }
                result = ratios[ib];
            }
        }
        ret[i] = result;
    }
    return ret;
};

1. Floyd算法
   优化查询次数

var calcEquation = function(equations, values, queries) {
    let nvars = 0;
    const variables = new Map();

    const n = equations.length;
    for (let i = 0; i < n; i++) {
        if (!variables.has(equations[i][0])) {
            variables.set(equations[i][0], nvars++);
        }
        if (!variables.has(equations[i][1])) {
            variables.set(equations[i][1], nvars++);
        }
    }
    const graph = new Array(nvars).fill(0).map(() => new Array(nvars).fill(-1.0));
    for (let i = 0; i < n; i++) {
        const va = variables.get(equations[i][0]), vb = variables.get(equations[i][1]);
        graph[va][vb] = values[i];
        graph[vb][va] = 1.0 / values[i];
    }

    for (let k = 0; k < nvars; k++) {
        for (let i = 0; i < nvars; i++) {
            for (let j = 0; j < nvars; j++) {
                if (graph[i][k] > 0 && graph[k][j] > 0) {
                    graph[i][j] = graph[i][k] * graph[k][j];
                }
            }
        }
    }

    const queriesCount = queries.length;
    const ret = new Array(queriesCount).fill(0);
    for (let i = 0; i < queriesCount; i++) {
        const query = queries[i];
        let result = -1.0;
        if (variables.has(query[0]) && variables.has(query[1])) {
            const ia = variables.get(query[0]), ib = variables.get(query[1]);
            if (graph[ia][ib] > 0) {
                result = graph[ia][ib];
            }
        }
        ret[i] = result;
    }
    return ret;
};

2923.找到冠军

题目：

一场比赛中共有 n 支队伍，按从 0 到 n - 1 编号。
给你一个下标从 0 开始、大小为 n * n 的二维布尔矩阵 grid 。对于满足 0 <= i, j <= n - 1 且 i != j 的所有 i, j ：如果 grid[i][j] == 1，那么 i 队比 j 队 强 ；否则，j 队比 i 队 强 。
在这场比赛中，如果不存在某支强于 a 队的队伍，则认为 a 队将会是 冠军 。
返回这场比赛中将会成为冠军的队伍。

---

解析：

本来只是个简单题，但是我觉得打擂台的思路很巧妙，记录一下。不用打擂台的话，有两种解法，i行的行和为n-1，代表i是冠军；j列中没有1，代表j是冠军

打擂台：假设冠军是 champ=0，我们从 i=1 开始遍历，寻找可以击败 cham的队伍，也就是 grid[i][champ]=1。

如果没有出现 grid[i][champ]=1，那么答案就是 champ，否则冠军可能是 i，更新 champ=i。然后从 i+1 继续向后遍历，因为 [1,i−1]中没有比 0 强的队，更别说比 i 强了。重复上述过程，最后返回 champ。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var findChampion = function(grid) {
    let champ=0;
    for(let i=1;i<grid.length;i++){
        if(grid[i][champ]){
            champ=i;
        }
    }
    return champ;
};

162.寻找峰值

题目：

峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

---

解析：

时间复杂度为 O(log n)一出，肯定是二分法，学一下爬坡法

在 [0,n) 的范围内随机一个初始位置 i，随后根据 nums[i−1],nums[i],nums[i+1]三者的关系决定向哪个方向走：

如果 nums[i−1]nums[i+1]，那么位置 i 就是峰值位置，可以直接返回 i 作为答案；

如果 nums[i−1]<nums[i]<nums[i+1]，那么位置 i 处于上坡，需要往右走，即 i←i+1；

如果 nums[i−1]>nums[i]>nums[i+1]，那么位置 i 处于下坡，需要往左走，即 i←i−1；

如果 nums[i−1]>nums[i]<nums[i+1]，那么位置 i 位于山谷，两侧都是上坡，可以朝任意方向走。

爬坡法为什么一定能找到山峰呢，一种通俗的理解是中点所在地方，可能是某座山的山峰，山的下坡处，山的上坡处，如果是山峰，最后会二分终止也会找到，关键是二分方向，并不知道山峰在我们左边还是右边，如果你往下坡方向走，也许可能遇到新的山峰，但是也许是一个一直下降的坡，最后到边界。但是如果你往上坡方向走，就算最后一直上的边界，由于最边界是负无穷，所以就一定能找到山峰，总的一句话，往递增的方向上，二分，一定能找到，往递减的方向只是可能找到，也许没有。

二分法最要注意的是区间问题，l和r带不带等号，mid+1还是-1，建议现场画图

/**
 * @param {number[]} nums
 * @return {number}
 */
var findPeakElement = function(nums) {
    let l=0,r=nums.length-1;
    while(l<r){
        let mid=Math.floor((l+r)/2);
        if(nums[mid]>nums[mid+1]){
            r=mid;
        }else{
            l=mid+1;
        }
    }
    return r;
};

2300.咒语和药水的成功对数

题目：

峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

---

解析：

注意一下二分的开闭区间问题

这里整理一下二分区间常见写法

1. [left, right]

int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }

1. [left, right)

int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }

本题用闭区间

/**
 * @param {number[]} spells
 * @param {number[]} potions
 * @param {number} success
 * @return {number[]}
 */
var successfulPairs = function(spells, potions, success){
    potions.sort((a,b)=>a-b);
    const binarySearch=(l,r,nums,target)=>{
        let res=r+1;
        while(l<=r){
            const mid=Math.floor((l+r)/2);
            if(nums[mid]>target){
                res=mid;
                r=mid-1;
            }else{
                l=mid+1;
            }
        }
        return res;
    }
    return spells.map((item) => {
        return potions.length - binarySearch( 0, potions.length - 1, potions,(success - 1) / item)
    })
};

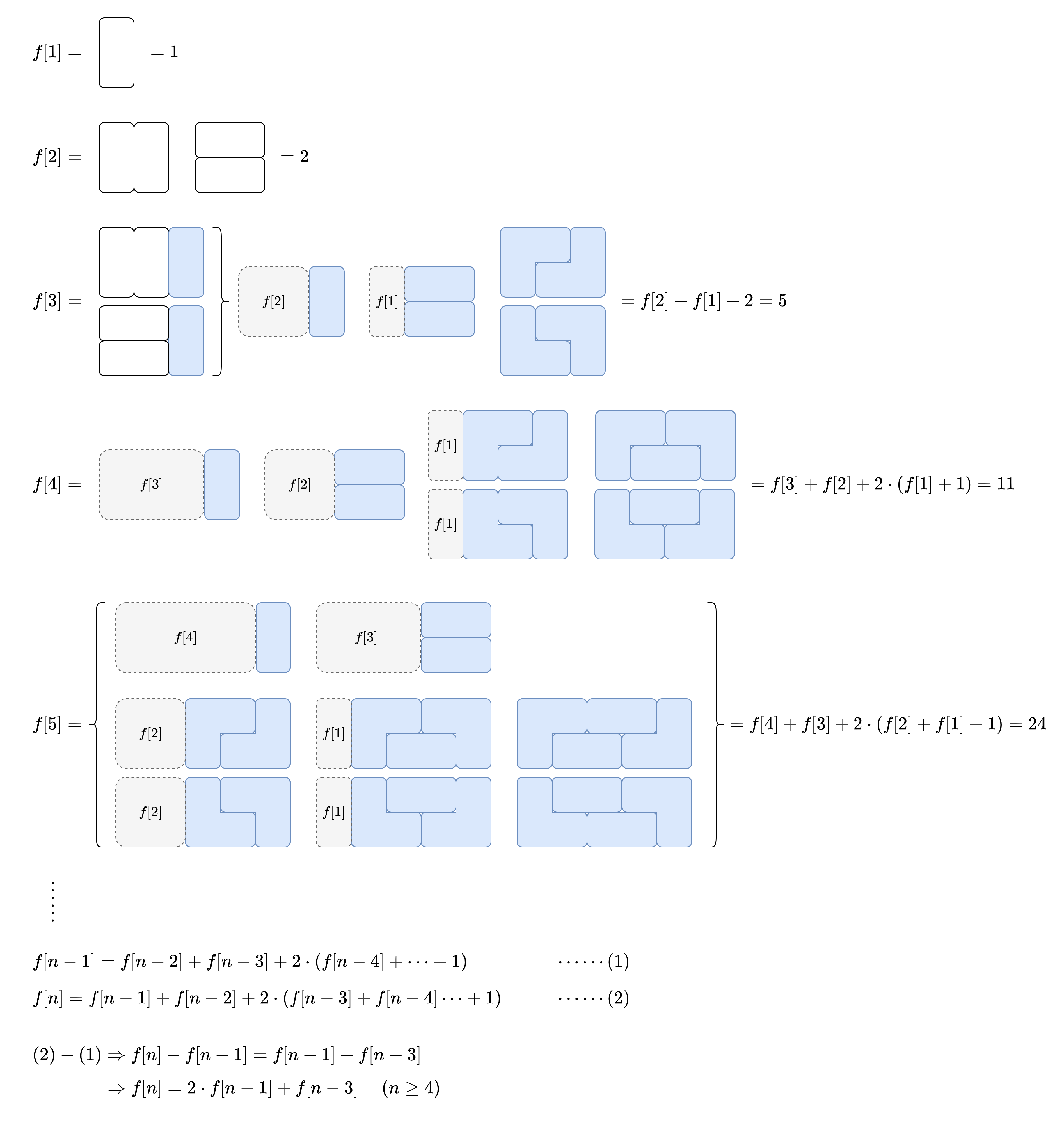
790.多米诺和托米诺平铺

题目：

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

---

解析：

1. dp
   这个方法得配图解释
   在第 i 列前面的正方形都被瓷砖覆盖，在第 i 列后面的正方形都没有被瓷砖覆盖（i 从 1 开始计数）。那么第 i 列的正方形有四种被覆盖的情况：

一个正方形都没有被覆盖，记为状态 0；

只有上方的正方形被覆盖，记为状态 1；

只有下方的正方形被覆盖，记为状态 2；

上下两个正方形都被覆盖，记为状态 3。

使用 dp[i][s] 表示平铺到第 i 列时，各个状态 s 对应的平铺方法数量。考虑第 i−1列和第 i 列正方形，它们之间的状态转移如下图（红色条表示新铺的瓷砖）：

var numTilings = function(n) {
    const mod = 1e9 + 7;
    const dp = new Array(n + 1).fill(0).map(() => new Array(4).fill(0));
    dp[0][3] = 1;
    for (let i = 1; i <= n; i++) {
        dp[i][0] = dp[i - 1][3];
        dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % mod;
        dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
        dp[i][3] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3]) % mod;
    }
    return dp[n][3];
};

1. 规律

/**
 * @param {number} n
 * @return {number}
 */
var numTilings = function(n) {
    const mod = 1e9 + 7;
    if (n == 1) return 1;
        let f = new Array(n + 1);
        f[0] = f[1] = 1;
        f[2] = 2;
        for (let i = 3; i <= n; ++i)
            f[i] = (f[i - 1] * 2 + f[i - 3]) % mod;
        return f[n];

};

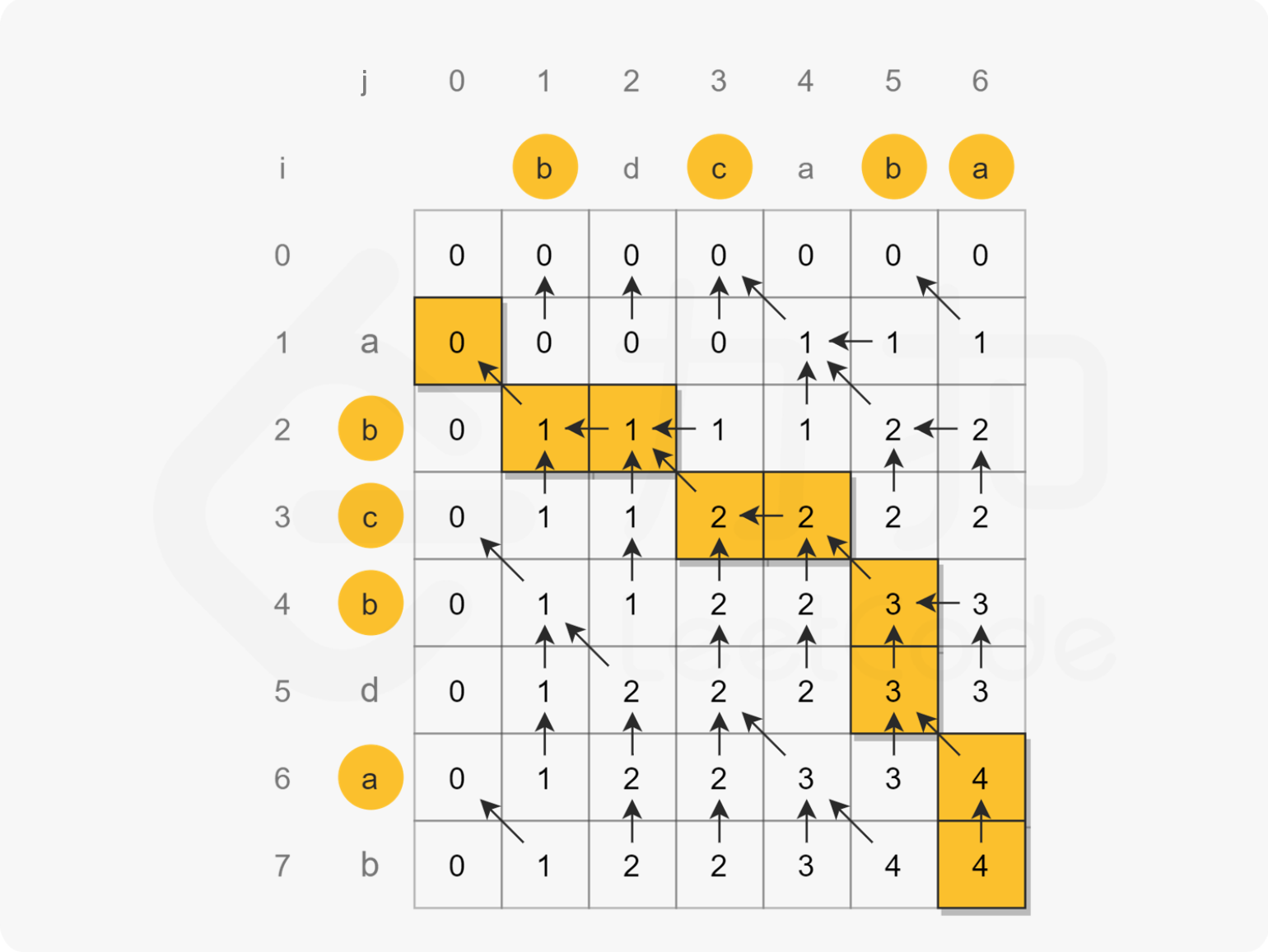
1143.最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

---

解析：

经典dp

dp[i][j] 表示 text1[0:i]和 text2[0:j]的最长公共子序列的长度

状态转移方程：

/**
 * @param {string} text1
 * @param {string} text2
 * @return {number}
 */
var longestCommonSubsequence = function(text1, text2) {
    let dp=new Array(text1.length+1).fill(0).map(()=>new Array(text2.length+1).fill(0));
    for(let i=1;i<=text1.length;i++){
        const ch=text1[i-1];
        for(let j=1;j<=text2.length;j++){
            if(ch==text2[j-1]){
                dp[i][j]=dp[i-1][j-1]+1;
            }else{
                dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
            }
        }
    }
    return dp[text1.length][text2.length];
};

714.买卖股票的最佳时机含手续费

题目：

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

---

解析：

1. dp

定义状态 dp[i][0]表示第 iii 天交易完后手里没有股票的最大利润，dp[i][1] 表示第 i 天交易完后手里持有一支股票的最大利润（i 从 0 开始）。

dp[i][0]=max{dp[i−1][0],dp[i−1][1]+prices[i]−fee}
dp[i][1]=max{dp[i−1][1],dp[i−1][0]−prices[i]}

/**
 * @param {number[]} prices
 * @param {number} fee
 * @return {number}
 */
var maxProfit = function (prices, fee) {
    let dp = new Array(prices.length).fill(0).map(() => new Array(2).fill(0));
    dp[0][0] = 0;
    dp[0][1] = -prices[0];
    for (let i = 1; i < prices.length; i++) {
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    }
    return dp[prices.length - 1][0];
};

//优化一下空间
var maxProfit = function (prices, fee) {
    [sell,buy]= [0, -prices[0]];
    for (let i = 1; i < prices.length; i++) {
        [sell,buy] = [Math.max(sell, buy + prices[i] - fee),Math.max(buy, sell - prices[i])];
    }
    return sell;
};

1. 贪心

不关心买卖的具体时间，只讲求每天的净利润最大

var maxProfit = function(prices, fee) {
    const n = prices.length;
    // 记录买入最低价格（加了手续费）
    let buy = prices[0] + fee;
    let profit = 0;
    for (let i = 1; i < n; i++) {
        //当前价格比之前买入时低，所以现在再买
        if (prices[i] + fee < buy) {
            buy = prices[i] + fee;
        } //当前价格比买入高，先假装卖掉
        else if (prices[i] > buy) {
            profit += prices[i] - buy;
            buy = prices[i];
        }
        //其余情况不动
    }
    return profit;
};

2542.最大子序列的分数

题目：

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，两者长度都是 n ，再给你一个正整数 k 。你必须从 nums1 中选一个长度为 k 的 子序列 对应的下标。
对于选择的下标 i_0 ，i_1 ，…， i_{k - 1} ，你的 分数 定义如下：
nums1 中下标对应元素求和，乘以 nums2 中下标对应元素的 最小值 。
用公式表示： 。
请你返回 最大 可能的分数。
一个数组的 子序列 下标是集合 {0, 1, …, n-1} 中删除若干元素得到的剩余集合，也可以不删除任何元素。

---

解析：

这题关键在怎么遍历两个数组可以保证遍历次数最少，这里先把要算最小值的nums2降序排列，保证nums2是从大到小一个一个遍历的，然后对nums1使用最小堆，保证每一次遍历sum一定会比之前的sum更大

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @param {number} k
 * @return {number}
 */
var maxScore = function(nums1, nums2, k) {
    const n = nums1.length;
    const ids = [...Array(n).keys()];
    // 对下标排序，不影响原数组的顺序
    //这里先把nums2从大到小排序，选取前k个，这时的nums2[ids[k-1]]就是前k个中最小的
    ids.sort((i, j) => nums2[j] - nums2[i]);

    const pq = new MinPriorityQueue();
    let sum = 0;
    //这里按照nums2的下标计算nums1对应的和，并把nums1对应下标的每个元素入最小堆
    for (let i = 0; i < k; i++) {
        sum += nums1[ids[i]];
        pq.enqueue(nums1[ids[i]]);
    }
    //对下标数组k之后进行遍历，如果后面下标对应的nums1的值大于当前和的最小堆的最小值，就替换最小值，比较更改后的乘积是否会更大
    let ans = sum * nums2[ids[k - 1]];
    for (let i = k; i < n; i++) {
        const x = nums1[ids[i]];
        if (x > pq.front().element) {
            sum += x - pq.dequeue().element;
            pq.enqueue(x);
            ans = Math.max(ans, sum * nums2[ids[i]]);
        }
    }
    return ans;
};

2462.雇佣k位工人的总代价

题目：

给你一个下标从 0 开始的整数数组 costs ，其中 costs[i] 是雇佣第 i 位工人的代价。
同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人：
总共进行 k 轮雇佣，且每一轮恰好雇佣一位工人。
在每一轮雇佣中，从最前面 candidates 和最后面 candidates 人中选出代价最小的一位工人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。
比方说，costs = [3,2,7,7,1,2] 且 candidates = 2 ，第一轮雇佣中，我们选择第 4 位工人，因为他的代价最小 [3,2,7,7,1,2] 。
第二轮雇佣，我们选择第 1 位工人，因为他们的代价与第 4 位工人一样都是最小代价，而且下标更小，[3,2,7,7,2] 。注意每一轮雇佣后，剩余工人的下标可能会发生变化。
如果剩余员工数目不足 candidates 人，那么下一轮雇佣他们中代价最小的一人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。
一位工人只能被选择一次。
返回雇佣恰好 k 位工人的总代价。

---

解析：

注意一下这个candidates是指从前数candidates个元素和从后数candidates个元素找这两个里面的最小值，所以用两个最小堆

/**
 * @param {number[]} costs
 * @param {number} k
 * @param {number} candidates
 * @return {number}
 */
var totalCost = function(costs, k, candidates) {
    let left = new MinPriorityQueue();
    let right = new MinPriorityQueue();
    let i = 0;
    let j = costs.length - 1;
    let ans = 0;
    while (k--) {
        while (i <= j && left.size() < candidates) {
            left.enqueue(costs[i++]);
        }
        while (i <= j && right.size() < candidates) {
            right.enqueue(costs[j--]);
        }
        let min1 = left.size() > 0 ? left.front().element : Infinity;
        let min2 = right.size() > 0 ? right.front().element : Infinity;
        if (min1 <= min2) {
            ans += left.dequeue().element;
        } else {
            ans += right.dequeue().element;
        }
    }
    return ans;
};

---

力扣75堂堂完结